Patricio Quezada Morales(1), Hernán Lara Padilla(2), Borys Hernán Culqui(3), Andrés Carrillo Albuja(4)
Universidad de las Fuerzas Armadas ESPE mpquezada@espe.edu.ec
Resumen
El presente trabajo muestra un enfoque holístico donde se aplica la Ingeniería Asistida por Computador en el diseño de membranas para el tratamiento médico conocido como regeneración guiada para el hueso de la zona alveolar/maxilar. Se propone el diseño de dos tipos de membranas, con y sin porosidad. Los diseños fueron modelados y simulados computacionalmente bajo condiciones de carga biomecánicas con comportamiento lineal. Ambos tipos de membrana presentan una resistencia mecánica superior a los valores reportados por la literatura. Este nuevo enfoque puede aportar a la optimización del diseño y la manufactura de injertos e implantes óseos en aplicaciones periodontales.
Palabras clave
ingeniería asistida por computador, regeneración guiada, membrana, alveolar, elemento finito.
Abstract
The current research presents a holistic approach wherein Computer-Aided Engineering was applied in the design of membranes for the medical procedure called guided bone regeneration for the alveolar/maxilla zone. Two kinds of membranes were proposed, with and without porosity. The designs were computationally simulated under biomechanics loads with linear behavior. In both cases, the membranes show a mechanical strength greater than the values reported in the literature. This new approach can help to the optimization of the design and manufacturing of grafts and implants for bone tissue in periodontal applications.
Keywords
Computer-Aided Engineering, guided regeneration, membrane, alveolar, finite element.
Introducción
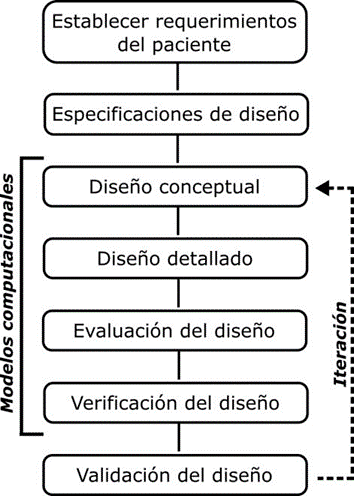
De acuerdo a la OMS la periodontitis afecta a un 20% de los adultos de edad media a nivel mundial y su padecimiento está asociado a varios factores de riesgo (“CDC: Half of American Adults Have Periodontal Disease | Perio.org”, 2017). Enfermedades como la periodontitis, osteoporosis y otras pueden afectar severamente a la zona basal de los huesos maxilares produciendo la pérdida de hueso en zonas aledañas a la dentadura, que a su vez puede ocasionar el desprendimiento de piezas dentales afectando severamente la salud bucal del paciente (Stavropoulos, 2008). Gracias a los avances en biomateriales, hoy en día existen procedimientos que pueden regenerar hueso en la zona maxilar restaurando la funcionalidad y apariencia. Sin embargo, aún persisten riesgos asociados con este tipo de tratamientos debido a (i) procesos quirúrgicos para colocar y retirar un sistema o membrana de soporte, (ii) reacción fisiológica al injerto osado para la regeneración ósea, (iii) reacción fisiológica al material de la membrana al no ser completamente biocompatible y reabsorbible, y (iv) cargas mecánicas por efectos de los movimientos de masticación. Con los avances en medicina regenerativa, nuevos conceptos y desarrollos de materiales han surgido en la última década (Asa’ad et al., 2017). Es así que el uso de membranas o andamios basados en materiales biocompatibles y bioabsorbibles han incursionado en el tratamiento de defectos óseos. Dependiendo del tipo de defecto y la ubicación en el cuerpo humano diferentes materiales pueden ser usados tales como cerámicos (Fosfatos de calcio, hidroxiapatitas y Bioglass®), polímeros (policaprolactona, colágeno, PLGA) y metales (titanio, acero inoxidable, magnesio) y combinaciones de ellos. Procesos de manufactura avanzados también han surgido como necesidad de fabricar partes como sustitutos óseos que tengan propiedades específicas como mecánicas (elasticidad, resistencia mecánica), físicas (porosidad, permeabilidad, tortuosidad), biológicas (biocompatibilidad, biodegradabilidad), entre otras. El diseño asistido por computador (CAE) y el método del elemento finito (FEM) ha interesado a los investigadores de la odontología debido a la necesidad de diseñar y simular computacionalmente fenómenos físicos y biológicos asociados con implantes e injertos, este proceso se ha visto favorecido por el alto desarrollo de los sistemas computacionales (Figura 1). El método del elemento finito ha permitido obtener un mejor entendimiento de los esfuerzos producidos en un implante o injerto y en el hueso u otros tejidos a su alrededor (Cho, Huh, Kim, & Park, 2012). En este trabajo se presentan los principales aspectos considerados en el modelado biomecánico de una membrana para el tratamiento conocido como regeneración guiada de tejido buscando parámetros para optimizar su diseño y comportamiento luego de ser implantado. Se analizan dos modelos como prueba de concepto.
Materiales y Métodos
2.1 Regeneración guiada
El procedimiento de regeneración guiada de tejido es usado en tratamientos periodontales para permitir la regeneración del tejido óseo de zonas afectadas por resorción ósea debido a varios cuadros clínicos (Figura 2-a). El procedimiento en términos generales consiste en la colocación de una membrana alrededor de la zona afectada, la cual actúa como barrera entre la encía y el espacio vacío donde se regenerará nuevo hueso. En casos críticos se suele acompañar el tratamiento con injerto en forma de polvo para ayudar a la regeneración ósea. Una vez completado el tratamiento, la membrana debe ser retirada. La membrana cumple funciones vitales dentro de este procedimiento clínico, a saber, debe proporcionar un soporte mecánico adecuado para impedir que la encía produzca un aplastamiento en dirección de la pieza dental lo cual pudiera ocasionar que el hueso nunca se regenere, debe soportar cargas transmitidas por la pieza dental por efecto de fuerzas de masticación, impedir la generación de esfuerzos termomecánicos por efecto de cambios de temperatura que pueden producirse en la zona bucal, el material de la membrana debe ser completamente biocompatible para impedir reacciones adversas como irritación o dolor, y ser de fácil remoción al terminar el tratamiento. Este último punto es el que ha llevado a varios investigadores en buscar biomateriales que tengan la capacidad de resorberse fisiológicamente dentro del cuerpo humano, evitando de esta forma cirugías post-implantación que pueden afectar considerablemente la salud del paciente.
2.2 Modelo computacional de membrana para regeneración guiada
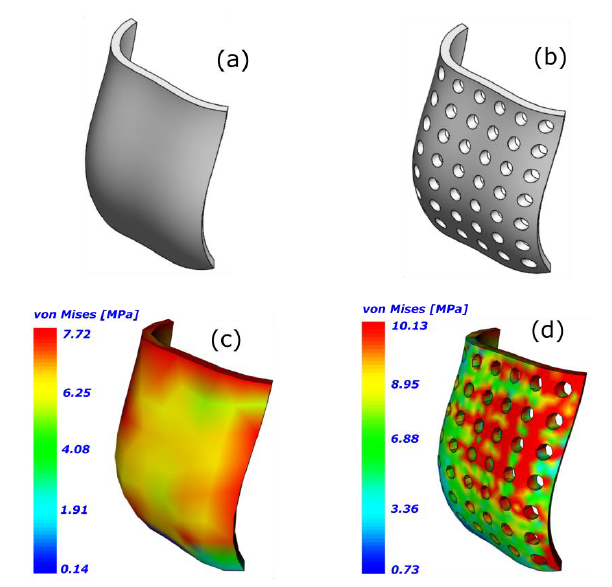
El esquema propuesto consiste en estudiar dos tipos de membranas semirígidas denominadas M1 (membrana sin porosidad) (Figura 3-a) y M2 (membrana con 50 % de porosidad con tamaño de poro de 1mm) (Figura 3-b). El diseño de la membrana está basado en imágenes médicas para el tratamiento de un paciente adulto. Las imágenes fueron procesadas en el programa BoneJ (Doube et al., 2010) para obtener el perfil aproximado de la membrana. El modelo CAD de la membrana fue desarrollado usando el método de superficies NURBS con la ayuda del plugin Grasshopper (http://www.grasshopper3d.com) para el programa Rhinoceros (https://www.rhino3d.com/).

Figura 2. Proceso para colocar una membrana para regeneración ósea en la zona periodontal
2.3 Ecuaciones constitutivas del modelo
Para determinar los esfuerzos a los cuales las membranas se hallan sometidos se empleará la formulación de la ley constitutiva para materiales que exhiben un comportamiento elástico lineal. La ley de Hook generalizada cuya linealidad relaciona los esfuerzos con la deformación infinitesimal a través del tensor de módulo elástico C:
𝜎𝑖𝑗=𝐶𝑖𝑗𝑚𝑛𝜀𝑚𝑛 (1)
Donde es el tensor de esfuerzos, es el tensor de deformaciones, y es el tensor de cuarto orden de constantes específicas del material. El tensor de constantes puede ser reducido a sólo dos parámetros independientes, λ y µ, también conocidas como constantes de Lamé, con su ecuación constitutiva dada por:
𝜎𝑖𝑗=𝜆𝜀𝛼𝛼𝛿𝑖𝑗+2𝜇𝜀𝑖𝑗 (2)
Donde representa la traza de, y es el operador delta de Kronecker. La ecuación (2) describe la ley constitutiva para un sólido isotrópico Hookeano, con λ conocido como el primer parámetro de Lamé y µ a menudo es referido como el módulo de corte. Otra forma de escribir la ley constitutiva es:

(3)
Donde E es el módulo de Young (o módulo de elasticidad), y es el coeficiente de Poisson. Uno de los indicadores representativos del esfuerzo mecánico es el esfuerzo de von Mises, cuya ecuación es:

(4)
El superíndice D indica que las componentes deviatorias del tensor de esfuerzo son consideradas.
2.4 Implementación numérica
El modelo numérico fue calculado usando el software ElmerGUI (https://www.csc.fi/web/elmer). Las membranas fueron modeladas usando elementos sólidos tipo tetraedro usando un factor general de malla de 0.2 mm. Para la simulación numérica una combinación de cargas debido a fuerzas de masticación y presión del lado de la encía fueron aplicados. El material considerado para el estudio fue la policaprolactona (PCL), un polímero semi cristalino biodegradable con temperatura de fusión de ≈60 °C y una temperatura de transición vítrea de ≈-60 °C. El módulo elástico y el coeficiente de Poisson considerados para la simulación numérica fueron 400 MPa y 0.33, respectivamente (Almeida, & Bártolo, 2013).
Resultados y discusión
El hueso en su estado normal es un tejido dinámico que se halla en una frecuente reabsorción y formación, permitiendo el mantenimiento de la estructura ósea del cuerpo humano. La función de remodelación dura toda la vida, sin embargo, a partir de los treinta años la tasa de reabsorción supera a la de formación. La pérdida de hueso en la zona maxilar se hace más evidente a partir de la tercera década y puede verse afectada aún más por enfermedades o malos hábitos. Han existido investigaciones por muchas décadas en búsqueda de lograr materiales biofuncionales que se adapten adecuadamente al paciente sin producir complicación alguna, pero aún existen áreas de estudio que buscan desarrollar mejores productos (Asa’ad et al., 2017).
En el presente estudio se han propuesto dos tipos de diseño, el primero es una membrana sin poros, la cual puede soportar mejor las cargas mecánicas (factor de seguridad aproximado de 1.3) (Figura 3-c) y por tanto permitir una regeneración adecuada de la zona alveolar, sin embargo, la falta de porosidad ocasiona que la permeabilidad de la membrana tienda a cero, lo que puede ocasionar algún tipo de inflamación debido a la falta de difusión de nutrientes entre el tejido blando (encía) y el tejido duro (hueso alveolar). Las membranas porosas por otra parte permiten una transferencia de nutrientes y señales biomecánicas adecuada, pero en ocasiones tienden a no regenerar completamente la zona afectada debido a la formación de concentradores de tensión alrededor de los poros. En el caso de estudio presentado el factor de seguridad en varias zonas es menor a la unidad (Figura 3-d).
En el campo de la regeneración guiada, Fujihara desarrolló membranas usando PCL y carbonato de calcio fabricadas mediante la técnica de electrohilado. Estas membranas constituidas por nanofibras presentaron una resistencia a tensión entre 2.8 y 4.8 MPa (Hammerle, Jung, & Feloutzis, 2002). Ueyama fabricó membranas de alginato con una resistencia máxima entre 8 y 34 kPa (Ueyama et al., 2002). Shim fabricó membranas de PCL y poli(ácido lático-co-ácido glicólico) (PLGA) usando las técnica de prototipado rápido reportando un módulo elástico de aproximadamente 50 Mpa y 700 MPa para PCL y PLGA, respectivamente (Shim et al., 2013). Won fabricó membranas mediante la técnica de impresión 3D usando colágeno y una mezcla de PCL, PLGA y β-TCP obteniendo una máxima carga de tensión de 69 N para el colágeno y 16 N para la mezcla (Won et al., 2016). Hammerle presenta datos de ensayos clínicos en diferentes condiciones donde se ha demostrado que el procedimiento de la regeneración guiada para hueso ha resultado exitoso (Hammerle, Jung, & Feloutzis, 2002).
A partir del presente estudio se puede destacar que el proceso usado para el diseño y la simulación de las membranas para regeneración guiada ha permitido desarrollar modelos computacionales paramétricos y que pudieran adaptarse a cambios de diseño, material o condiciones fisiológicas. Prueba de ello es que las cargas elásticas máximas soportadas por los modelos son mayores a los expuestos por la literatura.
En trabajos futuros se pretende fabricar las membranas a través de técnicas avanzadas de prototipado con diversas combinaciones de biomateriales y evaluaciones in-vitro. El horizonte del desarrollo de este tipo de implantes es combinar materiales y procesos buscando aplicar los diseños conocidos como multifásicos, en los cuales están presentes diferentes escalas: macro, micro y nano; este tipo de materiales multifásicos junto a la adición de factores de crecimiento e incorporación de fármacos finalmente permitirán tener productos que sean confiables para aplicaciones clínicas.
Conclusiones
Mediante un caso de estudio, la metodología CAE ha sido aplicada al área de biomedicina en el diseño de membranas para regeneración ósea de la zona alveolar. Se estudiaron dos tipos de membranas, con y sin porosidad para determinar la influencia de las cargas biomecánicas presentes durante la etapa de regeneración ósea. Los modelos propuestos presentan una adecuada resistencia mecánica en comparación con estudios previos. La convergencia de diversas disciplinas, en este caso ingeniería mecánica con biomedicina, pueden ayudar a acelerar los procesos de fabricación con biomateriales permitiendo una gama más amplia de aplicaciones con alta confiabilidad y seguridad para los pacientes.
Lista de Referencias
Almeida, H., & Bártolo, P. (2013). Numerical simulations of bioextruded polymer scaffolds for tissue engineering applications. Polymer International, n/a-n/a. http://dx.doi.org/10.1002/pi.4585
Asa’ad, F., Pagni, G., Pilipchuk, S., Giannì, A., Giannobile, W., & Rasperini, G. (2017). 3D-Printed Scaffolds and Biomaterials: Review of Alveolar Bone Augmentation and Periodontal Regeneration Applications. Retrieved 1 May 2017, from
CDC: Half of American Adults Have Periodontal Disease | Perio.org. (2017). Perio.org. Retrieved 1 May2017, from https://www.perio.org/consumer/cdc-study.htm
Cho, L., Huh, Y., Kim, D., & Park, C. (2012). Finite Element Analysis of Stress Distribution around
Patterned Implants. Journal Of Korean Dental Science, 5(1), 13-20. http://dx.doi.org/10.5856/jkds.2012.5.1.13
Ciocca, L., Fantini, M., De Crescenzio, F., Corinaldesi, G., & Scotti, R. (2017). CAD–CAM prosthetically guided bone regeneration using preformed titanium mesh for the reconstruction of atrophic maxillary arches. Retrieved 1 May 2017, from
De Boever, A., & De Boever, J. (2005). Guided bone regeneration around non-submerged implants in narrow alveolar ridges: a prospective long-term clinical study. Clinical Oral Implants Research, 16(5), 549-556. http://dx.doi.org/10.1111/j.1600-0501.2005.01154.x
Doube, M., Kłosowski, M., Arganda-Carreras, I., Cordelières, F., Dougherty, R., & Jackson, J. et al. (2010). BoneJ: Free and extensible bone image analysis in ImageJ. Bone, 47(6), 1076-1079. http://dx.doi.org/10.1016/j.bone.2010.08.023
Fujihara, K., Kotaki, M., & Ramakrishna, S. (2005). Guided bone regeneration membrane made of polycaprolactone/calcium carbonate composite nano-fibers. Biomaterials, 26(19), 4139-4147. http://dx.doi.org/10.1016/j.biomaterials.2004.09.014
Hammerle, C., Jung, R., & Feloutzis, A. (2002). A systematic review of the survival of implants in bone sites augmented with barrier membranes (guided bone regeneration) in partially edentulous patients. Journal Of Clinical Periodontology, 29(s3), 226-231. http://dx.doi.org/10.1034/j.1600-051x.29.s3.14.x
Shim, J., Huh, J., Park, J., Jeon, Y., Kang, S., & Kim, J. et al. (2013). Fabrication of Blended Polycaprolactone/Poly (Lactic-Co-Glycolic Acid)/β-Tricalcium Phosphate Thin Membrane Using Solid Freeform Fabrication Technology for Guided Bone Regeneration. Tissue Engineering Part A, 19(3-4), 317-328. http://dx.doi.org/10.1089/ten.tea.2011.0730
Stavropoulos, A. (2008). Deproteinized Bovine Bone Xenograft. Musculoskeletal Tissue Regeneration, 119-151. http://dx.doi.org/10.1007/978-1-59745-239-7_7
Ueyama, Y., Ishikawa, K., Mano, T., Koyama, T., Nagatsuka, H., Suzuki, K., & Ryoke, K. (2002). Usefulness as guided bone regeneration membrane of the alginate membrane. Biomaterials, 23(9), 2027-2033. http://dx.doi.org/10.1016/s0142-9612(01)00332-5
Won, J., Park, C., Bae, J., Ahn, G., Kim, C., & Lim, D. et al. (2016). Evaluation of 3D printed PCL/PLGA/β-TCP versus collagen membranes for guided bone regeneration in a beagle implant model. Biomedical Materials, 11(5), 055013. http://dx.doi.org/10.1088/1748-6041/11/5/055013

